Chủ đề: nguyên hàm 1 trên x bình: nguyên hàm 1 trên x bình là một khái niệm quan trọng trong tính toán và giải tích. Đây là công cụ giúp chúng ta tìm ra nguyên hàm của một hàm số dựa trên quy tắc đơn giản và dễ áp dụng của đạo hàm. Việc tìm nguyên hàm giúp chúng ta hiểu sâu hơn về tính chất và biểu đồ của một hàm số. Sử dụng nguyên hàm 1 trên x bình, ta có thể tính được diện tích và tích phân của một hàm số trong một khoảng xác định.
Nguyên hàm là gì?
Nguyên hàm là một khái niệm trong tính toán và toán học. Một nguyên hàm của một hàm số f(x) là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x). Khi đó, ta ký hiệu F(x) = ∫f(x)dx.
Để tìm nguyên hàm của một hàm số, ta thường áp dụng các công thức tính nguyên hàm đã biết và các phương pháp quy tắc.
Như trong trường hợp tìm nguyên hàm của hàm số f(x) = x - 1/x^2, ta sẽ áp dụng các quy tắc sau:
- Đối với hàm số x^n, nguyên hàm của nó là (x^(n+1))/(n+1) + C, với C là một hằng số.
- Đối với hàm số 1/x^n, nguyên hàm của nó là - (x^(1-n))/(1-n) + C, với C là một hằng số.
Áp dụng các quy tắc trên, ta có:
∫(x - 1/x^2)dx = ∫(x^1 - 1/x^2)dx = (x^2/2) + (1/x) + C, với C là một hằng số.
Tuy nhiên, trong một số trường hợp, việc tính nguyên hàm có thể phức tạp hơn và yêu cầu sử dụng các phương pháp khác nhau như phép thử và sai, phép đổi biến số, tích phân bằng phần, phép tính phụ, hoặc tích phân không gian. Việc tìm kiếm các công thức và phương pháp hợp lý là một phần quan trọng trong việc giải các bài toán tích phân và tìm nguyên hàm.
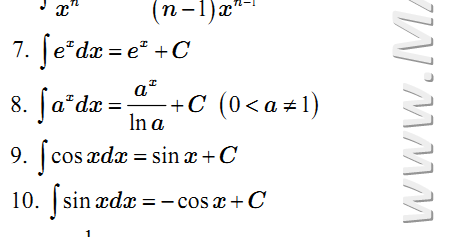

Cách tìm nguyên hàm của một hàm số?
Để tìm nguyên hàm của một hàm số, chúng ta cần tìm một hàm số khác sao cho khi tích phân của hàm số đó, kết quả sẽ là hàm số ban đầu.
Ví dụ, để tìm nguyên hàm của hàm số f(x) = x - 1 / x^2, ta sẽ làm như sau:
1. Đầu tiên, phân rã hàm số f(x) thành tổng của các hàm số đơn giản hơn. Trong trường hợp này, ta có thể phân rã f(x) thành 2 thành phần: x và 1 / x^2.
2. Tính nguyên hàm của từng thành phần. Trong trường hợp này, nguyên hàm của x là (1/2)x^2 và nguyên hàm của 1 / x^2 là -1 / x.
3. Kết hợp kết quả từ các bước trên, ta có nguyên hàm của hàm số ban đầu f(x) là F(x) = (1/2)x^2 - 1 / x.
Nguyên hàm F(x) này thoả mãn điều kiện rằng khi tích phân của nó, kết quả sẽ là hàm số ban đầu f(x).

Tính chất của nguyên hàm và đạo hàm?
Nguyên hàm được định nghĩa là một hàm số F(x) sao cho F\'(x) = f(x), trong đó f(x) là hàm số cần tính nguyên hàm.
Tính chất của nguyên hàm và đạo hàm gồm:
1. Tính đồng dạng: Nếu F(x) là một nguyên hàm của f(x), thì F(x) + C cũng là nguyên hàm của f(x), với C là một hằng số bất kỳ.
2. Tính chất dẫn suy: Nếu F(x) là một nguyên hàm của f(x), thì F(x) + C là nguyên hàm của f(x) trên mọi khoảng K, nơi K là tập hợp của các số thực.
3. Tính chất liên tục: Nếu f(x) có thể tích phân thành một nguyên hàm F(x) trên khoảng K, thì F(x) là một hàm liên tục trên K.
4. Tính chất tích phân: Dựa vào tích phân định nghĩa, ta có thể tính nguyên hàm của hàm số theo công thức Newton-Leibniz: ∫[a,b] f(x)dx = F(b) - F(a), trong đó F(x) là nguyên hàm của f(x).
5. Tính đối xứng: Nếu f(x) là một nguyên hàm của hàm số f(-x), thì F(x) + C cũng là nguyên hàm của f(x), với C là một hằng số bất kỳ.
Hy vọng thông tin trên sẽ giúp bạn hiểu rõ hơn về tính chất của nguyên hàm và đạo hàm.
Ứng dụng của nguyên hàm trong tính toán và vật lý?
Nguyên hàm (hay còn gọi là tích phân không xác định) được sử dụng rộng rãi trong tính toán và vật lý để giải quyết các bài toán liên quan đến tìm diện tích, tìm thể tích, tính lượng mật độ, tính vận tốc, tính gia tốc, và nhiều ứng dụng khác.
Trong tính toán, nguyên hàm được sử dụng để tính diện tích dưới đường cong của một hàm số trong một khoảng xác định. Việc tính diện tích này có thể áp dụng cho các bài toán như tính diện tích một hình dạng, diện tích giữa hai đường cong, diện tích của hình phẳng được giới hạn bởi các đường thẳng và đường cong.
Trong vật lý, nguyên hàm được sử dụng để tính toán các thông số quan trọng như vận tốc và gia tốc. Ví dụ, biết công thức gia tốc là đạo hàm của vận tốc theo thời gian, ta có thể tính được vận tốc bằng cách tích phân ngược lại công thức gia tốc.
Ngoài ra, nguyên hàm còn được sử dụng để tính toán tổng của một chuỗi số vô hạn. Đây là một ứng dụng quan trọng trong lĩnh vực chuỗi và dãy số của toán học.
Tóm lại, nguyên hàm có nhiều ứng dụng quan trọng trong tính toán và vật lý. Việc hiểu và ứng dụng nguyên hàm đúng cách sẽ giúp ta giải quyết các bài toán phức tạp và có thể tìm ra những ứng dụng mới trong các lĩnh vực khác.
Ví dụ minh họa về tính toán nguyên hàm của hàm số nguyên hàm 1 trên x bình.
Để tính nguyên hàm của hàm số \"nguyên hàm 1 trên x bình\", ta áp dụng định nghĩa của nguyên hàm.
Nguyên hàm của một hàm số là một hàm số khác mà đạo hàm của nó trùng với hàm số ban đầu.
Trong trường hợp này, chúng ta muốn tính nguyên hàm của hàm số f(x) = 1/x^2.
Để làm điều này, chúng ta sẽ sử dụng quy tắc tính nguyên hàm của các hàm số mũ. Biểu thức chung cho nguyên hàm của hàm số mũ ax^n là:
∫(ax^n)dx = (a/(n+1))x^(n+1) + C,
trong đó C là hằng số.
Áp dụng quy tắc này vào hàm số f(x) = 1/x^2, ta có:
∫(1/x^2)dx = (1/(2+1))x^(2+1) + C
= (1/3)x^3 + C.
Vậy, nguyên hàm của hàm số \"nguyên hàm 1 trên x bình\" là F(x) = (1/3)x^3 + C, với C là hằng số tùy ý.
_HOOK_