Xốt Gia Vị Hoàn Chỉnh Barona - Sườn Xào Chua Ngọt - International Food Master
Gói 80g
Trực tiếp tương quan cho tới mạch số (bao bao gồm những khối hệ thống dùng số) là những số nhị phân nên từng vấn đề tài liệu mặc dù là con số, những chữ , những lốt, những mệnh lệnh sau nằm trong cũng cần ở dạng nhị phân thì mạch số mới nhất hiểu đi ra và xử lý được. Do cơ cần sở hữu quy lăm le phương pháp tuy nhiên những số nhị phân được dùng để làm biểu thị những tài liệu không giống nhau, sản phẩm là có không ít mã số (gọi tắt là mã) được sử dụng. Trước tiên mã số thập phân phổ biến nhất là mã BCD ( Binary Coded Decimal: mã số thập phân được mã hóa theo đuổi nhị phân ). Sự quy đổi thập phân thanh lịch BCD và ngược lại gọi là mã hoá và sự lặp mã.
Người tớ biểu thị những số thập phân kể từ 0 cho tới 9 bởi vì số nhị phân 4 bit có mức giá trị như bảng tiếp sau đây.
Bạn đang xem: Lý thuyết hệ thống số với các loại mã và phép chuyển đổi

Chúng tớ nên để ý rằng: mã BCD cần được ghi chép đầy đủ 4 bit và sự ứng chỉ được vận dụng mang lại số thập phân kể từ 0 cho tới 9, nên số nhị phân kể từ 1010 (= 1010) cho tới 1111 (= 1510) của số nhị phân 4 bit ko cần là mã BCD.
Khi quy đổi tương hỗ thân thích thập phân và BCD tớ thực hiện như ví dụ minh họa sau đây:
Ví dụ 1: Ðổi 48910 sang mã BCD
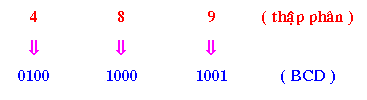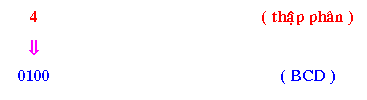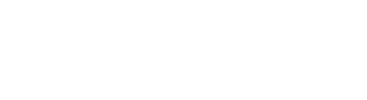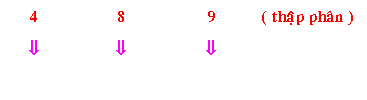
Ví dụ 2: Đổi 53710 sang mã BCD
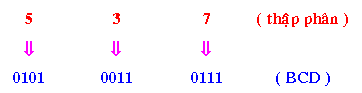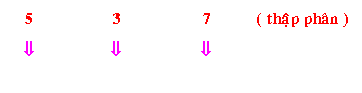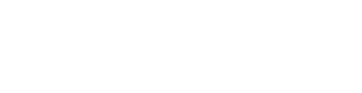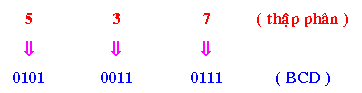
Ví dụ 3: Đổi 00110100100101012 (BCD) thanh lịch số thập phân
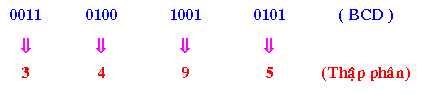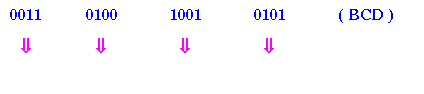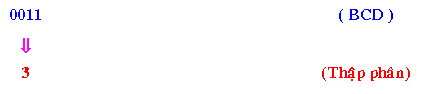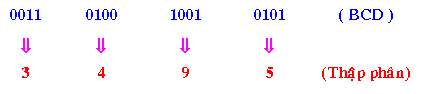
Điều cần thiết là cần quan sát rằng BCD ko cần là khối hệ thống số như khối hệ thống số thập phân, nhị phân, chén phân và thập lục phân. Thật đi ra, BCD là hệ thập phân với từng ký số được mã hóa trở thành độ quý hiếm nhị phân tương tự. Cũng cần hiểu rằng một trong những BCD ko cần là số nhị phân quy ước. Mã nhị phân quy ước trình diễn số thập phân hoàn hảo ở dạng nhị phân; Còn mã BCD chỉ quy đổi từng ký số thập phân thanh lịch số nhị phân ứng.
Mã BCD cần thiết nhiều bit rộng lớn nhằm trình diễn những số thập phân nhiều ký số (2 ký số trở lên trên. Vấn đề này là vì mã BCD ko dùng toàn bộ những group 4 bit rất có thể sở hữu, chính vì vậy sở hữu phần xoàng hiệu suất cao rộng lớn.
Ưu điểm của mã BCD là dể dàng quy đổi kể từ thập phân thanh lịch nhị phân và ngược lại. Chỉ chú ý những group mã 4 bit ứng với những ký số thập phân kể từ 0 cho tới 9.
Phối ăn ý những khối hệ thống số
Các khối hệ thống số vẫn trình diễn sở hữu côn trùng đối sánh tương quan như bảng sau đây:
Khi tổng nhỏ rộng lớn hoặc bởi vì 9 thì tớ tiến hành quy tắc nằm trong BCD như nằm trong nhị phân thông thường.
Ví dụ: xét quy tắc nằm trong 6 và 2, sử dụng mã BCD trình diễn côn trùng ký số
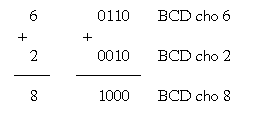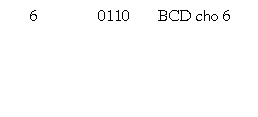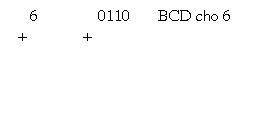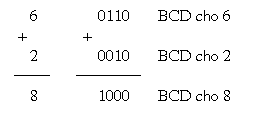
Một ví dụ không giống, nằm trong 45 với 33

Tổng to hơn 9
Ta xét quy tắc nằm trong 5 và 8 ở dạng BCD:
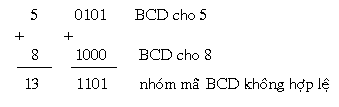
Tổng của quy tắc nằm trong phía trên là 1101 ko tồn bên trên vô mã BCD. Vấn đề này xẩy ra tự tổng của nhị ký số vượt lên trước vượt 9. Trong tình huống này tớ cần hiệu chỉnh bằng phương pháp thêm vào đó 6 (0110) vô nhằm mục tiêu tính cho tới việc bỏ lỡ 6 group mã ko hợp thức.
Ví dụ:
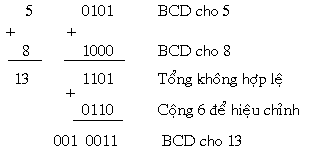
Một ví dụ khác:
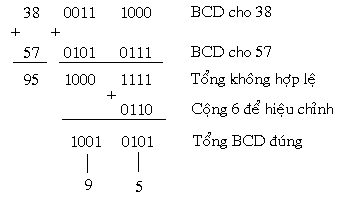
Mã chữ số được dùng rộng thoải mái nhất lúc bấy giờ là mã ASCII (American Standard Code for Information Interchange). Mã ASCII là mã 7 bit, nên sở hữu 27 = 128 group mã, đầy đủ nhằm biểu thị toàn bộ ký tự động của 1 bàn phím chuẩn chỉnh cũng như các công dụng tinh chỉnh và điều khiển. Bảng tiếp sau đây minh họa 1 phần list mã ASCII.
| Ký tự | Mã ASCII 7 bit | Bát phân | Thập phân |
| A
B C D E F G H I J K L M N O P Q R S T U V W X Y Z 1 2 3 4 5 6 7 8 9 <ký tự động riêng> . ( + $ * ) _ / , = <RETURN> <LINEFEED> |
100 0001`
100 0010 100 0011 100 0100 100 0101 100 0110 100 0111 100 1000 100 1001 100 1010 100 1011 100 1100 100 1101 100 1110 100 1111 101 0000 101 0001 101 0010 101 0011 101 0100 101 0101 101 0110 101 0111 101 1000 101 1001 101 1010 011 0000 011 0001 011 0010 011 0011 011 0100 011 0101 011 0110 011 0111 011 1000 011 1001 010 0000 010 1110 010 1000 010 1011 010 0100 010 1010 010 1001 010 1101 010 1111 010 1100 010 1101 000 1101 000 1010 |
101
102 103 104 105 106 107 110 111 112 113 114 115 116 117 120 121 122 123 124 125 126 127 130 131 132 060 061 062 063 064 065 066 067 070 071 040 056 050 053 044 052 051 055 057 054 075 015 012 |
41
42 43 Xem thêm: Cách viết địa chỉ bằng tiếng Anh dễ nhất | ZIM Academy 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F 50 51 52 53 54 55 56 57 58 59 5A 30 31 32 33 34 35 36 37 30 39 20 2E 28 2B 24 2A 29 2D 2F 2C 2D 0D 0A |
Bảng tiếp sau đây cho thấy mã số quá 3 ứng với số thập phân kể từ 0 cho tới 9. Để quy đổi số thập phân thanh lịch mã thứa 3 trước tiên tớ thêm thắt 3 vô số thập phân cơ rồi gửi thanh lịch nhị phân thông thường.
Ví dụ:
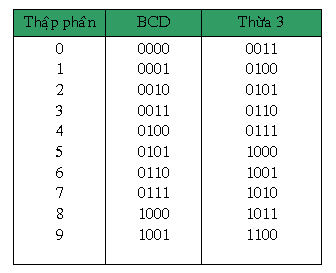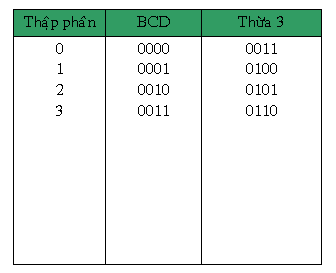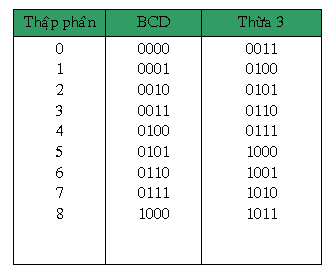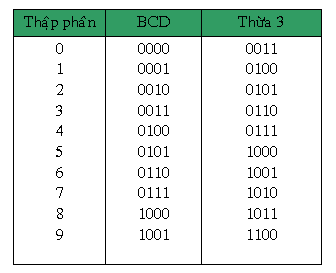
Do cơ hội ghi chép số thập phân đi ra mã quá 3 tương tự động như cơ hội ghi chép số thập phân đi ra mã BCD vẫn thưa ở trước, nên người tớ rất có thể hiểu mã quá 3 là một trong dạng của mã BCD. Để dể phân biệt mã BCD vẫn nói đến việc ở trong phần trước được gọi là mã BCD 8421.
Bảng tiếp sau đây trình diễn mã số Gray cùng theo với mã số nhị phân và thập phân kể từ 0 cho tới 15. Mã Gray được lựa chọn sao mang lại chỉ thay cho thay đổi một địa điểm bit thân thích nhị mã kế tiếp nhau.
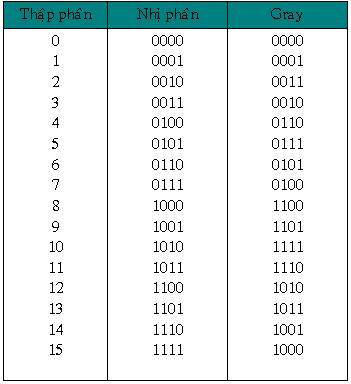
Tín hiệu biểu thị số nhị phân truyền kể từ mạch này thanh lịch mạch không giống, và nhất là truyền ra đi bị méo dạng và nhiễm nhiễu khiến cho số nhị phân cảm nhận được rất có thể sai ví với số cần thiết truyền. Để xử lý hiện tượng lạ này người tớ thêm nữa mã ASCII 7 bit một bit chẳn lẻ (Parity bit) ở địa điểm sở hữu nghĩa tối đa (bên trái) để sở hữu tài liệu 8 bit (1 bit chẵn lẻ, 7 bit tài liệu gốc). Tại cách sử dụng lẻ (Odd parity) thì bit parity thay cho thay đổi nhằm thực hiện mang lại tổng số phủ một trong những byte là lẻ. Ví dụ:

Ở cách sử dụng chẵn (Even parity) thì bit parity thay cho thay đổi khiến cho tổng số bit một trong những byte là chẵn. Ví dụ:

Bằng những thuật toán, những mạch số tiếp tục điểm tổng số bit nằm trong loại vô byte cảm nhận được nhằm xử lý, nếu như tài liệu xử lý ko khớp với qui ước về bit chẵn lẻ, số cơ sẽ tiến hành mạch phân biệt là số bị sai.
Mỗi ký số nhị phân (bit) sở hữu một trọng số dựa vào địa điểm của chính nó. Bất kỳ số nhị phân nào thì cũng đều rất có thể thay đổi trở thành số thập phân tương tự bằng phương pháp với những trọng số bên trên những địa điểm sở hữu bit 1.
Để làm rõ rộng lớn tớ xét một vài ba ví dụ sau đây:
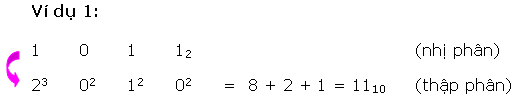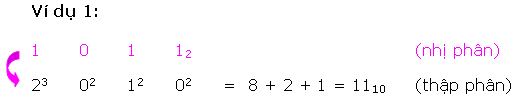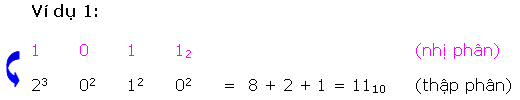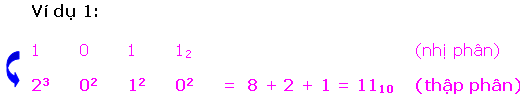
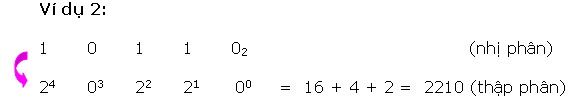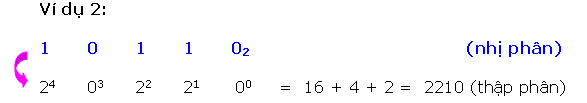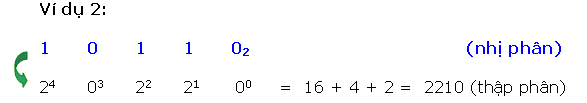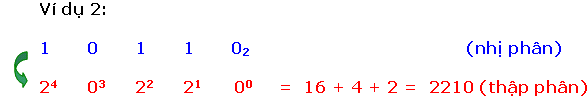
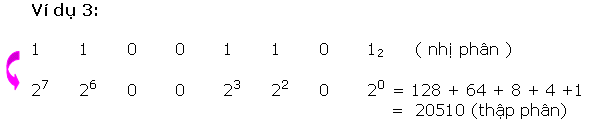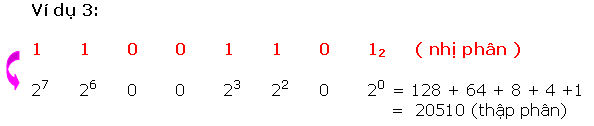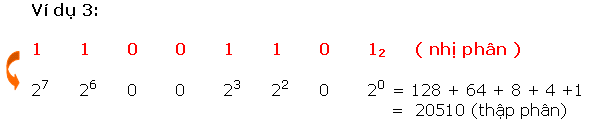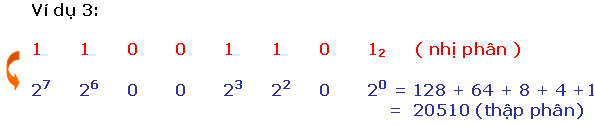
Có nhị cơ hội quy đổi một trong những thập phân thanh lịch nhị phân tương tự.
* Phương pháp loại nhất là cơ hội chuồn ngược lại quy trình thay đổi nhị phân thanh lịch thập phân, này đó là : số thập phân được trình diễn bên dưới dạng tổng những lũy quá của 2, tiếp sau đó ghi những kí số 0 và 1 vô địa điểm bit ứng.
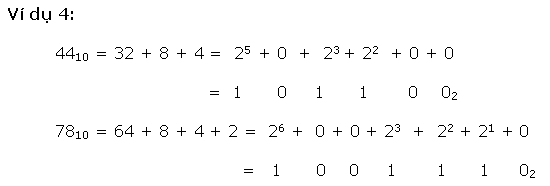
* Cách loại nhị canh ty quy đổi kể từ số thập phân nguyên vẹn thanh lịch nhị phân là sử dụng cách thức tái diễn quy tắc phân chia mang lại 2. Ví dụ, với một trong những thập phân 27 tớ tiến hành quy tắc phân chia số này mang lại 2 và ghi lại số dư sau từng chuyến phân chia cho tới Lúc nhận được thương số bởi vì 0, và sản phẩm nhị phân tạo hình bằng phương pháp ghi chép số dư trước tiên là LSB và số dư sau cuối là MSB.
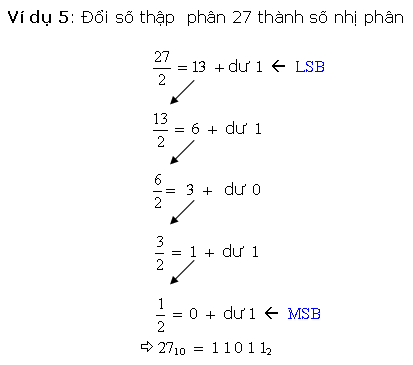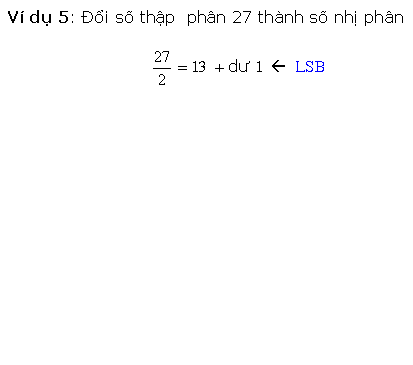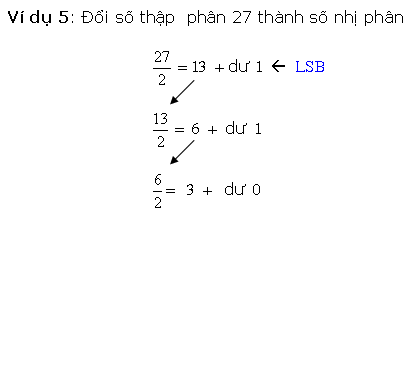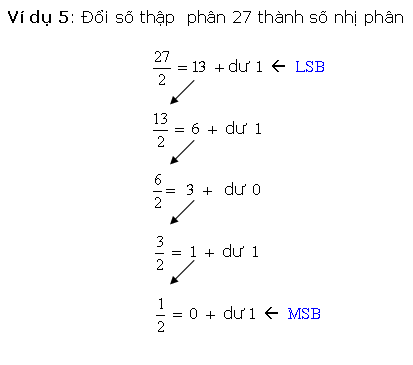
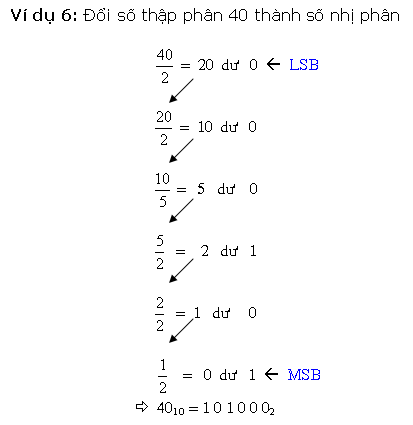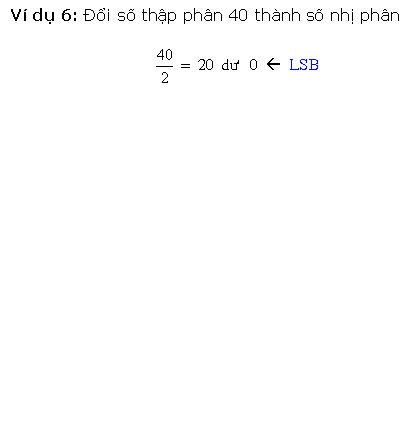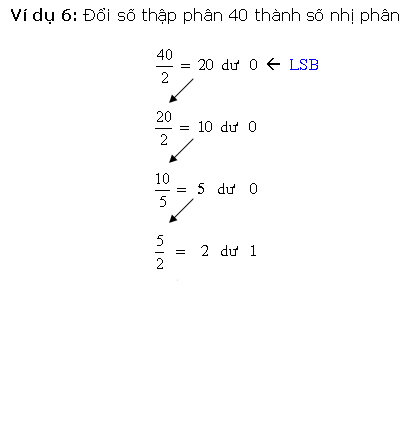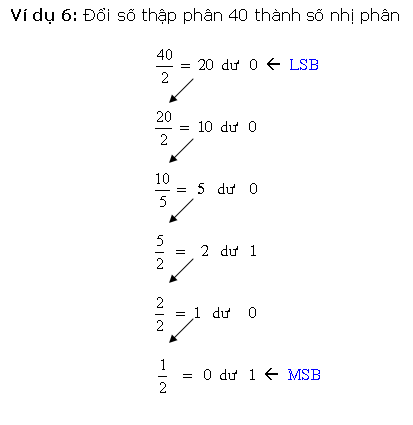
Quá trình quy đổi bởi vì cách thức này được minh họa bởi vì lưu đồ vật sau đây:
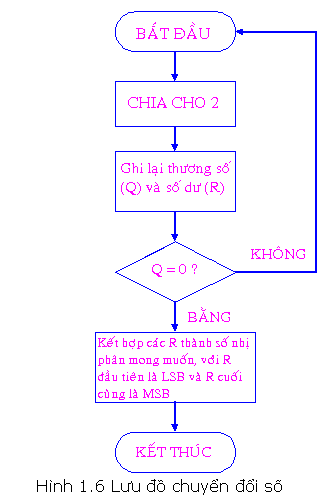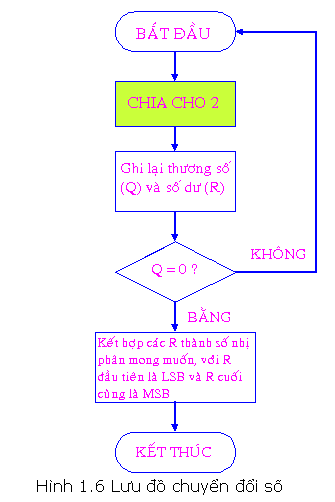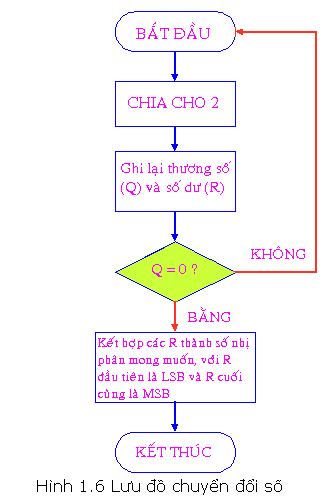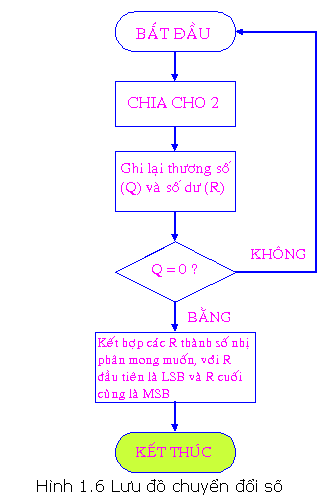
Lưu đồ vật bên trên biểu diển cách thức tái diễn quy tắc phân chia nhằm quy đổi số nguyên vẹn thập phân thanh lịch nhị phân. Phương pháp này cũng khá được dùng nhằm quy đổi số nguyên vẹn thập phân thanh lịch bất ký khối hệ thống số này không giống.
Ta dể dàng thay đổi số chén phân thanh lịch thập phân tương tự bằng phương pháp nhân từng ký số chén phân với trọng số của chính nó, rồi nằm trong sản phẩm cùng nhau.
Ví dụ 7: Đổi số chén phân 4708 trở thành số thập phân
4758 = 4x(82) + 7x(81) + 5x(80)
= 4×64 + 7×8 + 5×1
= 31710
Ví dụ 8: Đổi số chén phân 34.6 trở thành số thập phân
34.68 = 3x(81) + 4x(80) + 6x(8-1)
= 24 + 4 + 0.75
= 28.7510
Có thể sử dụng cách thức tái diễn quy tắc phân chia nhằm thay đổi một trong những nguyên vẹn thập phân thanh lịch chén phân tương tự, với số phân chia là 8.
Ví dụ 9: Đổi số thập phân 36510 trở thành số chén phân tương đương
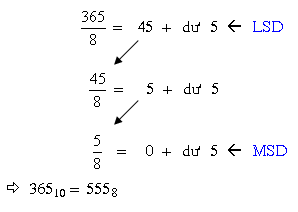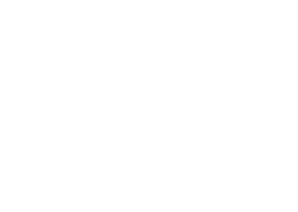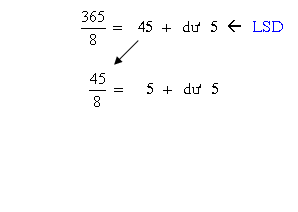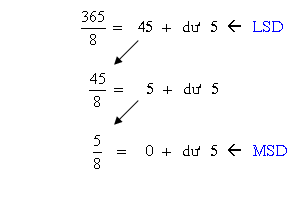
Chú ý một điều là: số dư trước tiên là số có mức giá trị nhỏ nhất (LSB) của số chén phân, số dư sau cuối là số có mức giá trị lớn số 1 (MSB) của số chén phân.
Phép thay đổi kể từ chén phân thanh lịch nhị phân đuợc tiến hành bằng phương pháp thay đổi từng ký số chén phân thanh lịch số nhị phân 3 bit tương tự. Tám ký số chén phân được thay đổi như bảng sau đây: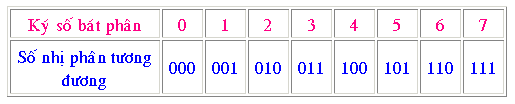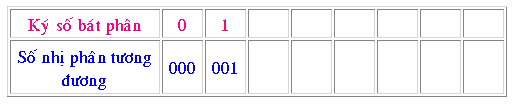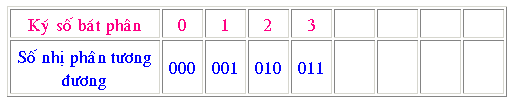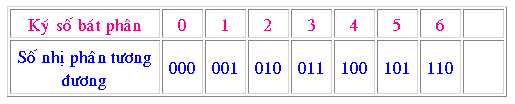
Ví dụ 10:
Đổi số 3468 sang nhị phân
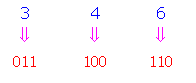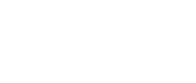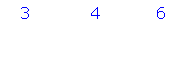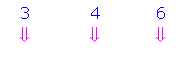
→Như vậy số chén phân 3468 tương đương với số nhị phân 0111001102
Đổi số 324710 thanh lịch nhị phân
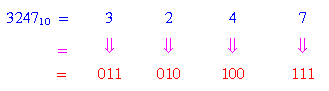
→Như vậy số chén phân 32478 tương tự với số nhị phân: 0110101001112
Đổi kể từ số nguyên vẹn nhị phân thanh lịch chén phân được thực hiêïn ngược lại với quy trình thay đổi kể từ chén phân thanh lịch nhị phân. Các bit của số nhị phân được group trở thành từng group 3 bit, chính thức kể từ LSB. Sau cơ từng group được thay đổi thanh lịch số chén phân tương tự.
Ví dụ 11: thay đổi số nhị phân 1001101102 trở thành số chén phân
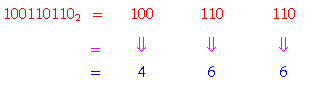
Như vậy số nhị phân 1001101102 tương tự với số chén phân 4668
khi ko đầy đủ 3 bit mang lại group còn sót lại, tình huống này tớ tiếp tục thêm 1 hoặc nhị bit 0 vô phía trái MSB của số nhị phân nhằm đầy đủ mang lại group sau nằm trong.
Ví dụ 14: thay đổi số 110111012 trở thành số chén phân
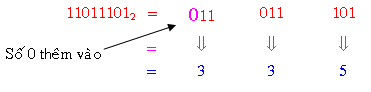
Cách điểm vô hệ chén phân: vô hệ chén phân ký số lớn số 1 là 7 chính vì vậy vô cơ hội điểm chén phân, địa điểm ký số tăng kể từ 0 cho tới 7, tiếp cơ tớ tái diễn kể từ 0 cho tới vòng sau đó và tăng địa điểm ký số lên 1.
Như vậy với N địa điểm số chén phân thì tớ rất có thể điểm kể từ 0 cho tới 8N – 1, tổng số sở hữu 8N số điểm không giống nhau. Ví dụ: với 4 địa điểm ký số chén phân tớ rất có thể điểm kể từ 00008 đến 77778.
Một số thập lục phân rất có thể được thay đổi trở thành số thập phân tương tự phụ thuộc tài liệu từng địa điểm ký số thập lục phân sở hữu trọng số là lũy quá 16. LSD sở hữu trọng số là 160, ký số thập lục phân ở địa điểm tiếp sau sở hữu số nón tạo thêm. Quá trình quy đổi như sau:
Ví dụ tớ thay đổi một trong những thập lục phân 45616 sang số thập phân tương tự tớ thực hiện như sau:
45616 = 4×162 + 5×161 + 6×160
= 4×256 + 5×16 + 6×1
= 1024 + 80 + 6
= 111010
Một ví dụ không giống thay đổi số thập lục phân 4BE16 thành số thập phân tương đương
4BE16 = 4×162 + 11×161 + 14×160
= 1024 + 176 + 14
= 121410
Chú ý, vô ví dụ thứ hai thay cho 11 vô B và 14 vô E Lúc thay đổi thanh lịch thập phân.
Theo cơ hội quy đổi như 2 ví dụ bên trên thì tớ rất có thể thay đổi ngẫu nhiên một trong những thập lục phân thanh lịch thập phân tương tự.
Tương tự động như cơ hội thay đổi kể từ thập phân thanh lịch nhị phân hoặc chén thân thích, Lúc thay đổi kể từ thập phân thanh lịch thập lục phân tớ cũng sử dụng cơ hội tái diễn quy tắc phân chia mang lại 16 và lấy số dư như trước.
Ví dụ 15: thay đổi số 76510 thành số thập lục phân.
Ta tiến hành quy tắc phân chia, tớ được:
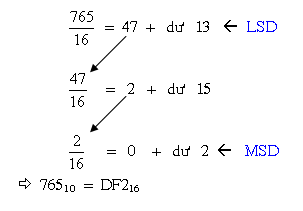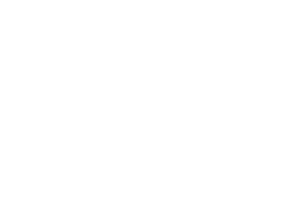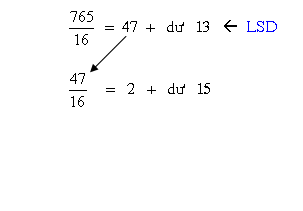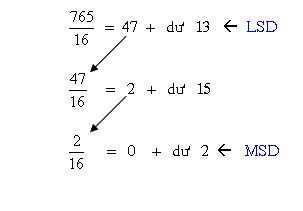
Ví dụ 16: Đổi 72410 thành số thập lục phân
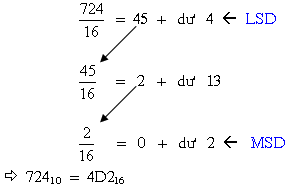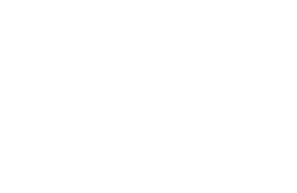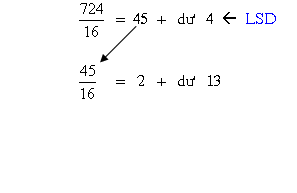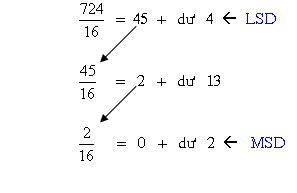
Chúng tớ nên lưu giữ rằng ngẫu nhiên một trong những dư nào vô quy tắc phân chia to hơn 9 đều được trình diễn bởi vì những chữ kể từ A cho tới F Lúc thay đổi thanh lịch số thập lục phân.
Cách thay đổi kể từ số thập lục phân thanh lịch số nhị phân cũng như thay đổi kể từ chén phân thanh lịch nhị phân, tức thị từng ký số thập lục phân được thay đổi thanh lịch độ quý hiếm nhị phân 4 bit tương tự.
Ví dụ 17: Đổi số 8D216
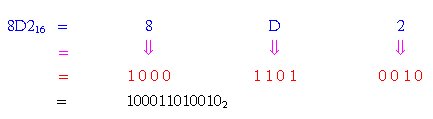
Để thay đổi kể từ số nhị phân thanh lịch thập lục phân tớ thực hiện ngược lại cơ hội thay đổi kể từ thập lục phân thanh lịch nhị phân. Nghĩa là tớ group trở thành từng group 4 bit, từng group được thay đổi thanh lịch ký số thập lục phân tương tự. Số 0 rất có thể được thêm nữa nhằm hoàn hảo 4 bit sau cuối.
Ví dụ 18 : Đổi số 110011011012 trở thành số thập lục phân
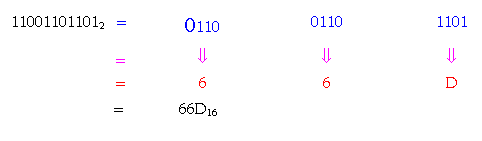
Ví dụ 19 : Đổi số 10101001112 trở thành số thập lục phân
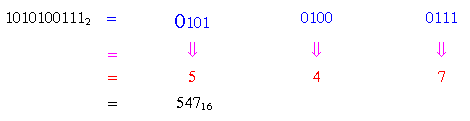
TÓM TẮT CÁC PHÉP CHUYỂN ĐỔI GIỮA CÁC HỆ THỐNG SỐ:
Phép nằm trong số hex được tiến hành tương tự như nằm trong thập phân. Sau đấy là phương pháp nhằm nằm trong số hex:
Cộng nhị ký số hex vô hệ thập phân, tính nhẫm độ quý hiếm thập phân tương tự mang lại những ký số to hơn 9
Nếu tổng nhỏ rộng lớn hoặc bởi vì 15, rất có thể trình diễn thẳng ở dạng ký số hex
Nếu tổng to hơn hoặc bởi vì 16, trừ 16 và lưu giữ 1 cho tới địa điểm ký số sau đó.
Sau đấy là một trong những ví dụ với những số hex minh họa
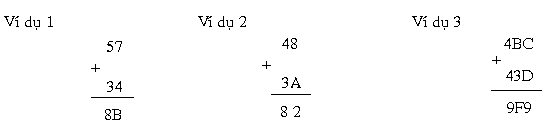
Ở ví dụ 1 tớ với những LSD (7 và 4) đã cho ra 11, là B ở hệ hex. Không sở hữu số lưu giữ, nằm trong 5 và 3 đã cho ra 8.
Ở ví dụ 2 tớ chính thức nằm trong 8 và A, tính nhẫm A đi ra độ quý hiếm thập phân là 10 . Do cơ tổng là 18, số này to hơn 16 nên tớ trừ mang lại 16 được 2, ghi chép số 2 và lưu giữ 1 thanh lịch địa điểm sau đó. Cộng số lưu giữ mang lại 4 và 3 tớ được tổng là 8.
Ở ví dụ 3 tổng của C và D coi như 12 + 13 = 2510, số này to hơn 16 nên tớ trừ mang lại 16 còn 9, và lưu giữ 1 thanh lịch địa điểm sau đó. Cộng số lưu giữ này với B và 3 tớ được 1510 đổi thanh lịch số hex là F , lưu giữ 1 thanh lịch địa điểm sau đó. Cộng số lưu giữ này với 4 và 4 tớ được 9, và sản phẩm sau cuối là 9F9.
Phép nằm trong nhị số nhị phân được tổ chức tương tự như nằm trong số thập phân. Các bước của quy tắc nằm trong nhị phân được vận dụng mang lại số nhị phân. Tuy nhiên, chỉ mất tư tình huống rất có thể xẩy ra vô quy tắc nằm trong nhị số nhị phân (bit) bên trên địa điểm ngẫu nhiên. Đó là:
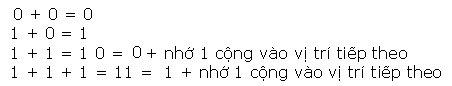
Dưới đấy là một vài ba ví dụ về nằm trong nhị số nhị phân (số thập phân tương tự vô lốt ngoặc):
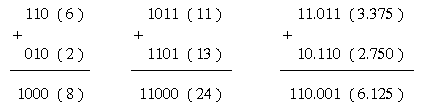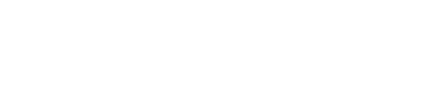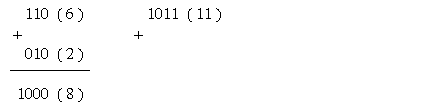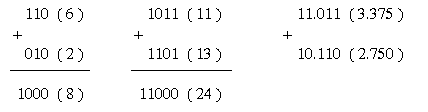
Phép nằm trong là quy tắc toán số học tập cần thiết nhất vô khối hệ thống nghệ thuật số. Như tớ tiếp tục thấy, những quy tắc trừ, nhân và phân chia được tiến hành ở đa số máy vi tính và PC bấm tay tân tiến nhất thực đi ra chỉ sử dụng quy tắc nằm trong thực hiện quy tắc toán cơ bạn dạng của bọn chúng.
Trong quy tắc trừ nếu như số trừ nhỏ rộng lớn số trừ, ví dụ là lúc 0 trừ 1, thì cần mượn 1 ở sản phẩm cao kế tiếp và là 2 ở ở sản phẩm đang được trừ và số mượn này cần trả lại mang lại sản phẩm cao kế tiếp tương tự động như quy tắc trừ của nhị số thập phân.
Ví dụ 1: tình huống trừ nhị số nhị phân 1 bit
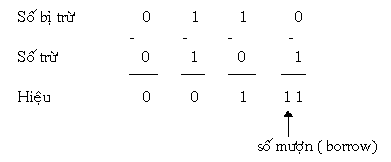
Ví dụ 2: Trừ nhị số nhị phân nhiều bit
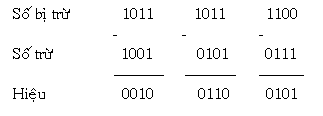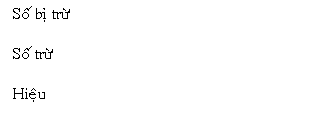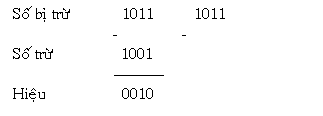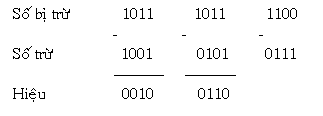
Do phần lớn PC xử lý cả số âm lẫn lộn số dương nên cần phải có tín hiệu này cơ nhằm biểu thị lốt của số ( + hoặc – ). Thông thường người tớ thêm thắt vào một trong những bit phụ gọi là bit lốt. Thông thường đồng ý bit 0 là bit lốt biểu thị số dương, bit một là bit lốt biểu thị số âm.
Dạng bù 1
Để sở hữu bù 1 của số nhị phân, tớ thay cho từng bit 0 trở thành bit 1 và từng bit 1 trở thành bit 0. Nói cách tiếp, tớ thay cho đỗi từng bit vô số nhị phân vẫn mang lại trở thành bit bù (đảo) ứng.
Ví dụ :

Dạng bù 2
Bù 2 của một trong những nhị phân được tạo hình bằng phương pháp lấy bù 1 của số và nằm trong 1 vô địa điểm nhỏ nhất.
Ví dụ 3: Tìm dạng bù 2 của số 1101012 = 5310

Ví dụ 4:

Biểu thao diễn số sở hữu lốt bởi vì bù 2
Bù 2 trình diễn những số sở hữu lốt Theo phong cách sau đây:
Nếu là số dương, thì trị vô cùng được trình diễn theo phương thức nhị phân thực sự của chính nó, và bit lốt là 0 được bịa đặt vô trước MSB.
Nếu là số âm, trị vô cùng được trình diễn ở dạng bù 2, và bit lốt là một trong được bịa đặt trước MSB.
Ví dụ minh họa:
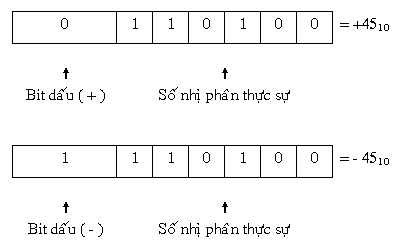
Các quy tắc tính vô bù 2 tương tự động như quy tắc tính số nhị phân thông thường.
Phép nhân số nhị phân được tiến hành tương tự động như nhân số thập phân. Quá trình thiệt đi ra đơn giản và giản dị rộng lớn vì như thế ký số của số nhân đơn giản 0 và 1, chính vì vậy tớ chỉ nhân mang lại 0 hay là một.
Ví dụ:

Phép phân chia một trong những nhị phân (số bị chia) mang lại một trong những không giống (số chia) được tiến hành tương tự như quy tắc phân chia số thập phân. Tiến trình thức tế còn đơn giản và giản dị rộng lớn tự Lúc đánh giá coi sở hữu từng nào chuyến số phân chia “ chuồn vào” số bị phân chia, chỉ mất nhị năng lực này đó là 0 và 1. Quá trình phân chia được minh họa bởi vì ví dụ sau:
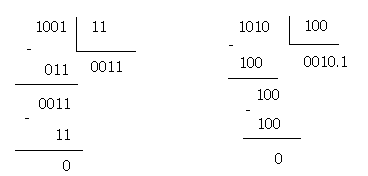
Xem thêm: Cách chơi Rubik 3x3 dễ hiểu nhất cho người mới
Trong ví dụ trước tiên tớ sở hữu 10012 chia mang lại 112, tương tự 910 chia mang lại 310
Thương số là 00112 = 310. Trong ví dụ thứ hai, 10102 chia mang lại 1002 tức là 1010 chia mang lại 410 kết trái ngược là 0010.12= 2.510
Phép phân chia số sở hữu lốt được tiến hành như quy tắc nhân. Số âm được trở thành số dương bởi vì quy tắc bù, tiếp sau đó mới nhất tiến hành quy tắc phân chia. Nếu số bị phân chia và số phân chia sở hữu lốt ngược nhau, thương số thay đổi thanh lịch số âm bằng phương pháp lấy bù 2 nó và gán bit lốt là một trong. Nếu số bị phân chia và số phân chia nằm trong lốt, thương số được xem là số dương và được gán bit lốt là 0.
Bạn có đang tìm kiếm các hình ảnh R%e1%ba%afn D%e1%bb%85 Th%c6%b0%c6%a1ng PNG hoặc vector ? Chọn từ 270000+ R%e1%ba%afn D%e1%bb%85 Th%c6%b0%c6%a1ng tài nguyên đồ họa và tải xuống dưới dạng PNG, EPS, AI hoặc PSD.
Download Phần Mềm khác tại: http://dienhathe.info Hotline: 0907 764 966 - email: [email protected] Auto Cad 2007
Máy tính điện tử khoa học Casio FX570VN PLUS
Cách tạo các công thức đơn giản trong Excel bằng cách dùng hàm AutoSum và SUM, cùng với cộng, trừ, nhân hoặc chia các giá trị trong trang tính của bạn.